基于多元统计分析的区域经济研究

　　0 引言

 

　　近十年随着中国的经济快速的增长,对于协调区域经济发展的研究也取得了一定的成果,陈斐等人[1]将空间统计分析嵌入到 GIS 系统中进行可行性分析.李雪梅等人[2]将主成分分析应用于区域经济分析中,吴涛等人[3]基于粗糙集理论对区域经济进行了分析.S.Luo[4]通过聚类分析研究中国区域经济.但是区域不平衡的现象并没有真正地解决,为了对每一类地区制定合适的经济发展的方案,本文对近几年中国的各类经济指标运用因子分析和回归分析方法进行了研究,确定了影响经济发展的因素并找到加快发展的动力.

 

　　1 分析方法的理论

 

　　本文在对区域经济的数据分析过程中采用了两种数据多元统计的方法,分别是因子分析法和回归分析法.因子分析(factor analysis)模型由主成分分析发展而来.在降低维度思想的基础上,将多个变量之间的复杂关系转变为少数因子的一种多变量统计分析的方法.与主成分分析方法相比,因子分析的特点是更注重于描述原始变量之间的相关关系.近年来随着数据挖掘技术的提高,人们将因子分析的理论成功地应用于经济学、心理学、医学等各个领域,不断丰富了因子分析的理论和方法.

 

　　回归分析属于统计学中的基本分析方法,一般用来确定因变量与若干个因素变量之间的关系表达式,通常称为回归方程或数学模型;此外,还可以通过控制可控变量的数值,通过建立的数学模型对因变量进行预测;回归分析还可进行因素分析,寻找出影响显着的变量,从而可以区别重要因素和次要因素.回归分析主要研究变量之间的线性关系因此又称为线性回归分析,多元线性回归的一般数学模型是:

 

　　Yi=茁0 茁1xi1 … 茁pxp1 着i,i=1,2,…,n (1)其中,xi1,xi2,…,xip分别是第 i 次的观测变量 x1,x2,…,xp的取值,Yi 为因变量 Y 的观测值,假定 着i(i=1,2,…,n)相互独立,且均服从同一正态分布 N(0,滓2),滓2是未知参数.回归分析需要对模型中的未知参数 茁0,茁1,…,茁p以及滓2做出估计,并且对建立的回归方程进行参数检验和设定检验,通过检验的模型可以用来解释现象或者对未来进行预测.

 

　　2 经济指标的选择

 

　　区域经济指的是在一定区域内经济发展的内部因素与外部条件相互作用而产生的生产综合体区域经济反应不同地区内经济发展的客观规律以及内涵和外延的相互关系.每一个区域经济的发展都受到自然条件、社会经济条件和技术经济政策等因素的制约.本论文以下 9 个经济发展的指标:

 

　　X1---工业增加值(亿元);X2---每万人拥有公共交通车辆(标台);X3---房地产开发企业个数(个);X4---城镇人口(万人);X5---批发零售业增加值(亿元);X6---居民人均储蓄(元);X7---金融业增加值(亿元);X8---全社会固定资产(亿元);X9---生产总值(亿元).

 

　　本文通过在国家数据统计局网站获得的 2015 年中国各省份的各个指标的原始数据作为经济分析的数据基础.

 

　　3 区域经济的数据分析

 

　　3.1 因子分析

 

　　本节主要应用因子分析的方法根据相关性大小对原始变量进行分组,从而提高同组内的变量之间相关性,通过该方法提取影响经济发展的主因子.将收集的资料导入数据分析软件 SPSS19.0,通过计算得出表 1 相关矩阵.从原始数据计算得到的相关矩阵可以总结得出,原始

 

 

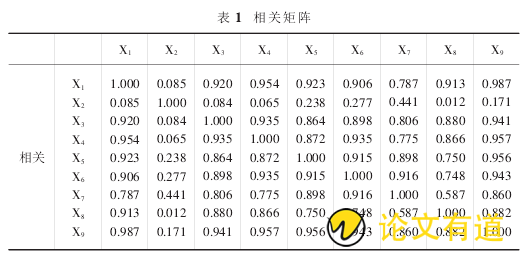
　　数据大部分变量的相关系数都大于 0.3,因此所搜集的原始数据可以采用因子分析的方法.

 

　　KMO 和 Bartlett 的检验表明,KMO 作为观测相关系数值和偏相关系数值的一个指标,KMO 值越大表明因子分析的相关性越强,因此越适合于作公共因子分析,获得的因子分析的结果越好,表 2 显示 KMO=0.808>0.5,说明原始数据适合做因子分析;Bartlett 的球形检验 P 值为0.000<0.05,也说明原始数据适合进行因子分子.从上面的三个方面来看,影响中国区域经济的各指标适合于因子分析,本节采用的方法是有效可行的.

 

 

　　表 3 为因子分析的解释总方差,选取的两个主成分F1、F2的方差占全部方差的比例为 92.978%,选取的主成分能够解释选取的 9 个变量的绝大部分,基本上是对原来指标的信息保留,并且将原指标的 9 个维度降为了 2 维,利于分析.

 

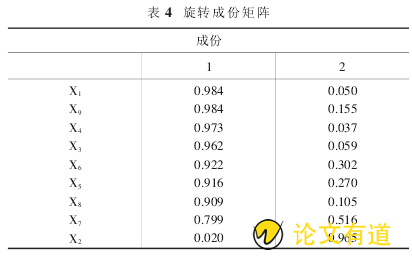
　　表 4 为旋转成分矩阵(Rotated Component Matrix),也为载荷矩阵,是一个系数矩阵,原变量可由各因子表示,如:X1=0.984×F′1 0.050×F′2,其矩阵模式:X=AF′.

 

 

　　因子得分和综合得分如表 5 所示.

 

　　通过上述因子分析得出的结果,大致可以将 2015 年全国区域经济划分为以下几类,如表 6 全国各省份因子分析所示.

 

 

　　从因素分析的结果来看,旋转后的因子载荷矩阵,公因子 F1′在 X1(工业增加值)、X3(房地产开发企业个数)、X4(城镇人口)、X5(批发零售增加值)、X6(居民人均储蓄)、X8(全社会固定资产)、X9(生产总值)上的载荷值很大,因此这 7 个经济指标的综合反映;公因子 F2′在 X2(每万人拥有公共交通车辆)、X7(金融业增加值)上的载荷值远远高于其他指标,这说明 F2′综合反映的是每万人拥有公共交通车辆、金融业增加值两个方面.

 

　　结合各个省份在公共因子和总得分情况,对全国各省份的发展情况进行评价.在经济方面综合指标 F1′得分最高的几个省份是江苏省、山东省、广东省;综合指标 F2′得分最高的是北京市和天津市;总得分最高的几个省份是江苏省、山东省、广东省这说明综合得分高的区县在选取的指标各方面发展比较均衡.

 

　　3.2 多元回归分析

 

　　通过对以上各省份的区域经济的划分,可以得出属于第三类地区的省份最多,为了实现我国经济的均衡发展必须大力促进第三类地区的省份的经济的发展,从因子分析的结果分析选取了三个因子得分较高的指标 X1(工业增加值)、X2(城镇居民人口数)、X3(房地产开发企业个数),为了便于分析第三类地区的经济发展状况这里以云南省为例,选取 2005-2015 近十年的数据,采用回归分析的方法建立回归模型,以便于对未来的生产总值做出预测.将数据导入 SPSS 软件中得到的分析结果如下:

 

 

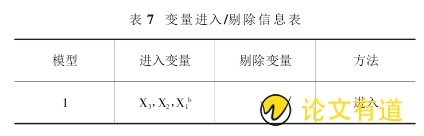
　　如表 7 所示,3 个自变量都进入模型,说明选取的解释变量都是显着并且是有解释力的.

 

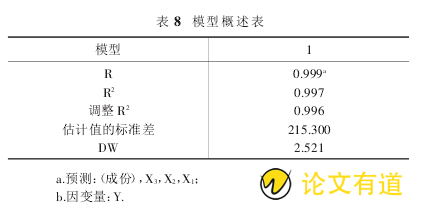
　　表 8 概述了模型整体拟合效果,模型的拟合优度系数为 0.999,反映因变量与自变量之间具有高度显着的线性关系.并且表中显示了 R 平方以及经调整的 R 值的估计标准误差,另外还得出了杜宾-瓦特森检验值 DW=2.521(DW 是用于检验一阶变量自回归形式的序列相关问题的统计量,DW 在数 2 到 4 之间说明模型无序列相关).

 

 

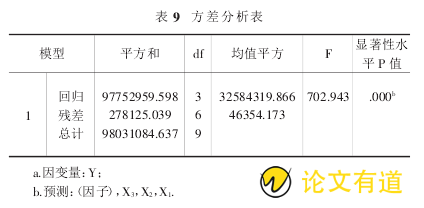
　　表 9 为分析方差分析表,可以得出模型的设定检验 F统计量的值为 702.943,显着水平的 P 值约等于零,于是所建模型通过了设定检验,说明因变量与自变量之间的线性关系明显.

 

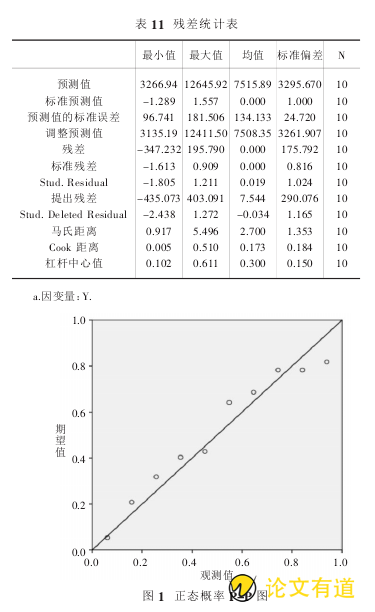
　　表 11 中显示了预测值、残差、标准化预测值、标准化残差的最小值、最大值、均值、标准差及样本容量等值,根据概率的 3 西格玛原则,标准化残差的绝对值最大为1.613,小于 3,说明样本数据中没有奇异值.

 

　　研究图 1 中的散点分布状况,10 个散点大致散布于斜线附近,因此可以认为残差分布基本上属于正态分布.

 

　　从回归系数表(表 10)中可以看出所建模型需要剔除变量 X3,用本次实验中使用的方法和步骤,重新使得 Y 对X1、X2回归,得到的主要结果如表 12-表 14 所示.

 

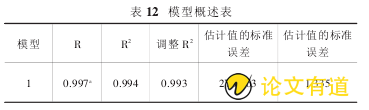
　　根据上面的分析结果,剔除 X3变量后,模型的拟合优度为 0.994 比原来有所降低;而 F 检验与通过了模型设定检验与原模型相同;新模型的各个系数都通过了显着性 T

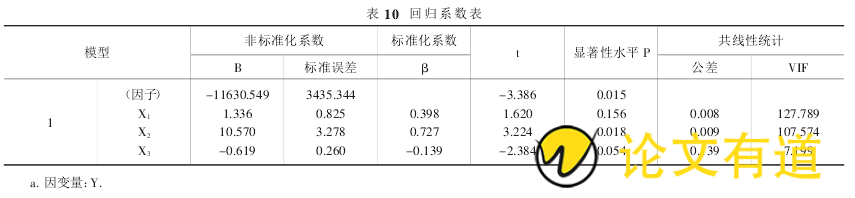
检验,因此更加合理,从而可以得出结论:剔除变量 X3后所建立的模型更加合理.

 

　　总结上述分析 得 到 的 回 归 系 数 b =(茁0,茁1,茁2)=(-14090.237,0.407,12.742),包含三个检验统计量,即相关系数平方 R2为 0.994,假设检验统计量 F 为 629.984,与F 对应的概率 P 为 0.000,从而得到初步回归方程:

 

　　Y=-14090.237 0.407X1 12.742X2

 

 

　　4 结果分析

 

　　通过以上的数据分析,可以得到区域经济的划分,无论是通过聚类分析得出的区域划分还是通过因子分析得出的区域划分都能够得出属于第三类地区的省份占到绝大多数,所以在进行经济战略部署的时候,应该以第一类地区的发展带动第三类地区的发展为重点才能够达到缩小经济区域发展差异的目标.通过区域的划分我们可以看到以下区域经济问题:①以广东、山东、江苏为首的发展迅速的三大省份,都是位于东部沿海地区,这说明中国沿海地区的省份拥有经济发展的资源更加的丰富,也可能在地区经济制度方面更加的完善,从而有利于该地区经济的发展.②从第二类地区中我们可以看到几乎包括了所有的直辖市,这说明该类地区的发展影响因素最大的应该是社会因素,人类的活动在促进经济发展方面起到了决定性的作用.③第三类地区的占到全国省份的 2/3,这些地区的地理条件有很大的差异,说明影响这些地区发展的因素是多方面的,不仅应该从自然条件方面找到制约经济发展的因素,还应该从社会资源等方面寻找该地区经济发展的瓶颈.

 

　　5 结语

 

　　我国的区域经济差异的因素虽然是多方面的但是也是有规律可循的,经过上述的数据分析在众多的指标中确定了影响经济发展的关键因素是工业生产增加值,所以应该从行业发展的状况中找到适合各类地区的有针对性的经济发展策略.以第一类地区作为全国经济发展的先锋,继续保持该地区省份的经济发展势头,整合该地区的各种发展资源,能够为第二、三类地区提供有效的经济发展资源,能够起到各地区相互帮扶的作用.为了加快第三类地区的经济发展,应该以第二类地区为联系的纽带,通过第一类地区对第二类地区的经济带动,进一步的使得第二类地区帮助第三类地区的发展,形成一个经济发展的链条.通过建立的回归分析模型可以得出城镇人口在促进经济发展的过程中起到了很大的作用,这也是国家要推进城市化建设的重要的原因,所以在今后的经济战略部署中应该加快各地区的城镇化建设,不断的增加城镇人口的数量.

 

　　参考文献:

 

　　[1]陈斐,杜道胜.空间统计分析与 GIS 在区域经济分析中的应用[J].武汉大学学报,2002,27(4):391-396.

　　[2]李雪梅,张素琴.主成分分析在区域经济分析中的应用[J].计算机工程与应用,2009,45(19):204-206.

　　[3]吴涛,陈黎伟,尚丽.基于粗糙理论的区域经济分析[J].运筹与管理,2007,16(5):90-95.

　　[4]S Luo. Clustering analysis of provincial economicdevelopment level of China [J].Journal of Chongqing Institute ofCommerce,2005.