【摘要】冷弯薄壁型钢由于其独特的成型特性在各领域都有广泛的应用。薄壁型钢处于不同的约束形式条件工作。在实际应用过程中,常常根据需要,在冷弯薄壁型钢腹板采用不同的支撑形式以及在不同位置采用机械方式冲剪不同直径的孔洞-带孔薄板。而在承受轴向压力载荷的情况下,带孔的薄壁型钢将具有不同的稳定性,并且当荷载增大到一定程度,可能发生屈曲破坏。针对受均布载荷下带孔薄壁板的弹性屈曲问题,通过有限元方法,研究方形薄板在不同支撑边界条件下及不同位置不同孔径的弹性屈曲特征性,以获取其屈曲临界载荷的变化规律及其对稳定性的影响。
【关键词】均布载荷;支撑形式;带孔薄板;弹性屈曲
1带孔薄壁钢板结构研究概况
薄壁钢构件由于易成型和易开孔等工艺特性在现代钢结构设计中应用非常广泛,如薄壁型钢组装的货架、电缆塔架以及船体内的格栅结构等。而在实际应用中不可避免地对薄壁型钢进行开孔,但以往的问题重点是对薄壁型钢杆件的弯曲和受压的屈曲。虽然对带孔薄壁钢板的研究较早[1-2],文献显示,大多是从载荷的作用形式等方面着手,且由于当时技术条件限制致使研究进展缓慢。M·Aydin Komur和Mustafa Sonmez[3]对中心处开有不同直径圆孔的方形薄板处于简支条件下,一对边分别作用集中载荷与局部均布载荷,且载荷沿着板边移动时,研究了其屈曲临界载荷的变化规律,得到在集中载荷从板边向中心移动过程中,屈曲临界载荷先增大后减小,且呈现类似正弦曲线特征的结论;同时在局部均布载荷下其屈曲临界载荷也呈现类似的规律;该研究并没有考虑不同边界支撑条件的情况。Khaled和Moham-mad[4]也通过有限元方法研究了对a=2b(a为长边长度,b为短边长度)的长方形简支薄板四边都作用均布载荷时,孔洞分别沿着长边和短边不同位置时的屈曲临界载荷的变化规律,结论为孔洞的直径越大,屈曲系数k越小,孔洞离载荷作用边越远,板的稳定性越高;这个研究同样也没有考虑不同边界支撑条件的情况。N·E·Shanmugan、V·Thevendran与Y·H·Tan[5]建立了带孔受压薄板的屈曲临界力的简易计算公式,这个公式考虑了带孔薄板的4种支撑形式,并且用ABAQUS软件与公式计算结果进行了验证,虽然结果吻合较好,但公式中的系数来源及其适用条件没有说明。在实际应用中,带孔薄板会根据不同情况采用不同的支撑形式,所以在研究带孔薄板的屈曲特性时应该考虑不同支撑形式的影响,而目前对不同支撑条件下带孔薄板的屈曲特性的研究成果仍然较少。
本文通过模拟工程上开孔薄板常用的4种支撑形式,采用有限元数值分析方法,在对有限元软件中不同板壳单元类型和网格划分方式对有限元数值分析结果精度的影响的同时,针对薄板在开孔孔径以及开孔位置不同时,分析开孔的孔径大小及位置对薄板屈曲临界载荷变化规律和稳定性的影响规律,以供相应支撑形式的薄板在进行开孔操作时参考。
2数值分析误差分析及网格划分
2.1软件ANSYS的适用性
ANSYS软件[6]是融结构、流体、电场、磁场、声场分析于一体的大型通用有限元分析软件,是现代产品设计中的高级CAE工具之一。在ANSYS中,稳定分析分为两类:线性或特征值屈曲分析和非线性屈曲分析。其中线性屈曲分析时线性或特征值屈曲分析考虑了应力刚化效应,这种效应会导致结构在承受应力后抵抗横向载荷能力降低,当压应力增加时,结构抵抗横向能力减小。在某一载荷水平下,这种负的应力刚度超过线性结构刚度,造成结构屈曲。屈曲发生的点称为分叉点,由于力-变形曲线达到该点后可能沿两条不同途径前进,所以当超过分叉点时,结构将屈曲或者在不稳定状态下承受载荷;而要精确地确定屈曲载荷,应该使用非线性屈曲分析。非线性屈曲分析中得出的极限载荷通常比线性屈曲分析确定的分叉点低。这是由于非线性屈曲能考虑真实结构中存在的初始缺陷,以及几何和材料的各种非线性。ANSYS程序在大变形分析中是把弧长法和Newton-Raphson法结合起来修正结构单元的方位,从而求出屈曲临界载荷。当单独使用增量Newton-Raphson法时,刚度矩阵可能会变成奇异矩阵。弧长法使Newton-Raphson平衡迭代沿一条弧收敛到其平衡路径。因此,可避免矩阵在那些奇异点处变为奇异矩阵,并控制收敛性。
2.2数值计算误差分析
软件ANSYS[6]进行带孔薄板的屈曲临界载荷分析中,两类因素对计算对结果有影响,一是由于网格尺寸的大小造成的计算误差,另一个是单元类型不同带来的计算误差。分析两类计算误差的影响程度,选取ANSYS软件中的SHELL63、SHELL181、SHELL2813种单元类型分别建模和进行屈曲计算,并通过结果进行对比分析,选择其中一种进行带孔薄板的屈曲临界载荷研究。
对比分析中采用各项同性材料,其弹性模量取E=201GPa,泊松比μ=0.3,板厚δ=1mm,板大小为a×b=100mm×100mm.为了保证所选单元和网格大小能够满足研究的需要,用四边简支的无孔板,一边受均布载荷作为比对标准。根据弹性力学[5]给出的屈曲临界载荷理论公式:
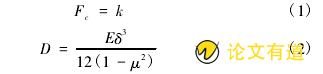
式中:k为屈曲系数,本文取k=4;μ为泊松比,取0.30;δ为板的厚度,本文取1mm;b为板边长,本文取100mm.
由式(1)、式(2)得到理论屈曲临界载荷为72593N.
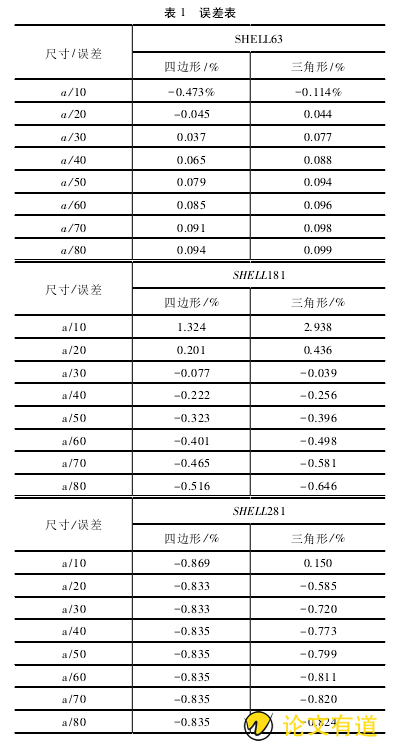
ANSYS软件分别用SHELL63、SHELL181、SHELL2813种单元模拟,分别采用四边形网格和三角形网格,并考虑了不同网格划分密度。表1汇总了不同单元类型、网格形状和尺寸的有限元计算结果和理论值之间的误差。
由表1可以看出,四边形网格时,SHELL63精度较高,SHELL281稳定性更高,三角形网格时SHELL281仍然体现了足够的稳定性,其他两个单元精度或稳定性较差。并且注意到当网格尺寸达到a/30时,计算的精度已经足够高。
2.3单元网格划分选用
考虑实际工程中板内开孔的不同情况,在网格划分时可能会出现三角形网格,需要关注计算分析的稳定性。综合考虑,本文分析时选用SHELL281单元,三角形网格,网格尺寸为a/30,以确保各单元的计算精度。有限元网格划分模型见图1.
3模型构建
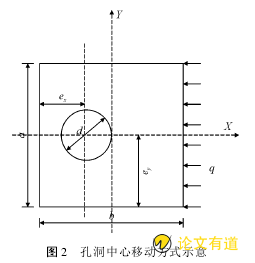
本文研究的重点是在均布载荷q作用下,不同直径的孔、孔中心在方板的中心线上分别沿X或Y轴上移动到对边时板的屈曲临界载荷变化规律(图2)。孔洞移动方式分两种情况,一种是孔中心沿着板的X轴方向移动(当孔中心落在Y方向中心,沿X方向从边4向边2移动称为X方向移动);一种是孔沿着Y方向移动(当孔中心落在X方向中心,沿Y方向从边1向边3移动称为Y方向移动)。
3.1参数选用
研究使用的材料是各项同性,弹性模量E=201GPa,泊松比μ=0.25,正方形板,边长a=b=100mm,板厚δ=1mm;孔直径d取5种大小的孔径,分别为d/a=0.05、0.1、0.15、0.2和0.25.孔中心到板边的距离为ex,X方向分取9个位置,ex/a=0.3、0.5、0.7、0.9、1.0、1.1、1.3、1.5和1.7;Y移动位置与X方向相同。
3.2边界条件
由于板的支撑条件对带孔板的屈曲临界力影响较大,所以对板每边的约束要明确指定以满足研究的需要。图3给出了采用的薄板支撑形式。
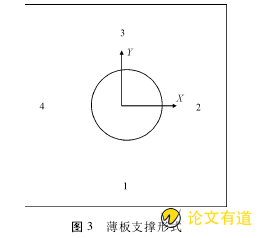
图3中的4种约束条件分别为:
(1)四边简支-支撑1:边1约束Z方向,边2约束Z方向,边3约束Y和Z方向,边4约束X和Z方向;
(2)三边简支、一边自由边-支撑2:边1为自由边;边2约束Z方向;边3约束Y和Z方向;边4约束X和Z方向;
(3)一边夹支、一边自由边-支撑3:边1为自由边;边2约束Z方向;边3约束Y和Z方向;同时约束X轴的转动;边4约束X和Z方向;
(4)两边夹支-支撑4:边1约束Z方向,同时约束X轴的转动;边2约束Z方向;边3约束Y和Z方向,同时约束X轴的转动;边4约束X和Z方向。
4不同约束条件计算结果分析
4.1四边简支孔板-支撑1
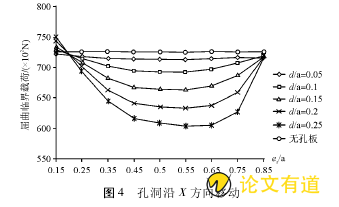
在薄板采用四边简支时,在孔洞沿X方向移动过程中,计算结果见图4.屈曲临界载荷先降低后升高,呈类似抛物线特征。孔在板的中心时屈曲临界载荷最小。经过与四边简支无孔板的临界荷载对比我们注意到,孔在ex/a=0.15附件时,带孔板的稳定性比无孔板的稳定性高,而且随着孔径增大稳定性也提高;当ex/a大于0.15时,带孔板稳定性比无孔板差,且开孔越大,屈曲临界载荷越小,当ex/a接近0.85时,屈曲临界载荷又趋于相同,并且接近于无孔板的屈曲临界载荷。
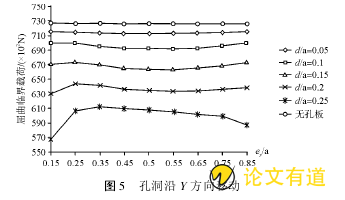
在孔沿着Y方向移动过程中,分析结果见图5.临界屈曲荷载明显低于四边简支无孔板的临界屈曲力荷载,板的稳定性降低,且孔径越大临界屈曲荷载越小。同时可以观察到,当孔径d/a小于0.15时,孔中心在Y轴上的位置对临界屈曲荷载影响不大。
4.2三边简支、一边自由边板-支撑2
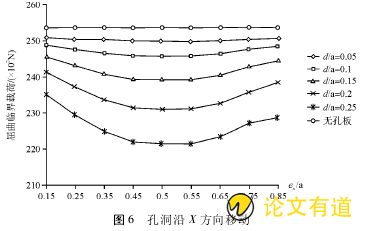
三边简支、一边自由边时,孔沿着X方向移动过程中,孔板的屈曲临界载荷先降低后升高,呈类似抛物线特征(图6),孔在板中心时,孔板的屈曲临界载荷最低。
当孔沿着Y方向移动过程中(图7),孔板的屈曲临界载荷逐渐增大。
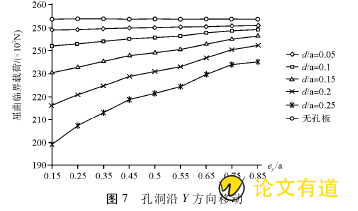
依据图6、图7的所示结果,无论孔洞沿X或Y方向移动,薄板采用支撑2时屈曲临界载荷均比无孔板小。
4.3一边夹支、一边自由边板-支撑3
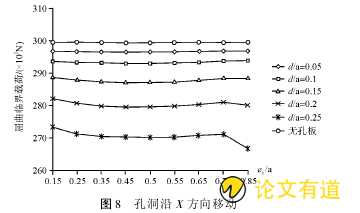
一边夹支、一边自由边时,孔沿着X方向移动过程中,屈曲临界载荷无明显变化(图8),屈曲临界载荷基本随孔洞的直径增大而降低,只有当ex/a=0.75后,屈曲临界载荷降低的比较明显。
当孔沿着Y方向移动过程中(图9),d/a=0.05的孔的屈曲临界载荷无明显变化,随着d/a增大,屈曲临界载荷逐步减低的幅度比较大,即孔径越大屈曲临界载荷越小;在相同的d/a时,却随着ey/a的增大,屈曲临界荷载有所逐步提高,在ey/a大于0.75后又呈减低趋势。
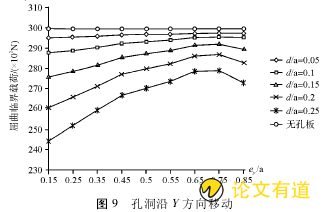
从图8、图9可看出,当薄板采用支撑3时,无论孔洞沿X或Y方向移动,屈曲临界载荷均比无孔板小。
4.4两边夹支板-支撑4
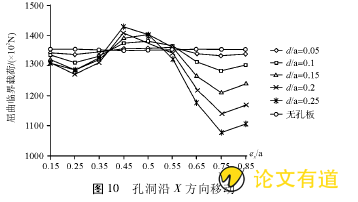
两边夹支的带孔板,孔沿着X方向移动过程中,屈曲临界载荷呈现类似正弦波的形状(图10),当孔在方板的中心附近时屈曲临界载荷最大;当ex/a大于0.60后,孔径越大,屈曲临界载荷越小。
当孔沿着Y方向移动过程中,屈曲临界载荷呈现类似抛物线特性(图11),孔在方板的中心附近时屈曲临界载荷最大,即随着ey/a的变化,屈曲临界载荷经历由小变大,但孔洞在板中心附近,屈曲临界载荷最大,随后又逐步减少。ey/a等于0.15和0.85时,随孔径增大,屈曲临界载荷越小。
依据图10、图11所示,孔洞在板边缘,其屈服临界荷载均小于无孔板;同时我们注意到,孔在板中心附近时,无论孔径大小,均比无孔板更加稳定。

5结论
通过有限元方法,分析a=b=100mm、δ=1mm的带孔薄板承受均布载荷、4种支撑形式时的屈曲临界荷载的变化规律,其中孔的直径d及孔的位置ex或ey是重要的控制变量,并可以得出以下结论:
(1)薄板采用支撑1时,在孔洞开在ex/a小于0.20位置,有助于提高板的稳定性,并且随孔径的增小稳定性越好。在其他位置开孔,无论孔的大小均比无孔板的稳定性差。
(2)薄板采用支撑2和支撑3的形式时,无论孔径的大小及在板中任何位置,板的稳定性都比无孔板有所降低,且孔径越大,板的稳定性越差。
(3)支撑3的形式,当ex/a=0.45~0.55时,带孔板的屈曲临界载荷最大,在该位置开孔比无孔板更稳定。当ex/a=0.75屈曲临界载荷最小,孔径越大屈曲临界载荷越小。
(4)支撑4与其他3种支撑对比发现,无论薄板孔径大小,只要开孔在板的中心附近,均可提高了薄板的稳定性。
(5)根据本文的研究,对方形薄板开孔并不一定降低薄壁型钢的稳定性,有时在适当位置开孔甚至有助于提高薄板的稳定性。
参考文献
[1]M·Z·Khan,K·C·Johns and B·Hayman,Buckling of plateswith partially loaded edges[J]. J.struct. Div,ASCE103. 1977:547-558.
[2]C·J·Brown,Elastic stability of plates subjected to concentratedloads[J]. Comput.Struct . 1989(33) :1325-1327.
[3]M·Aydin Komur,Mustafa Sonmez,Elastic buckling behavior ofrectangular plates with holes subjected to partial edge loading[J].Journal of Constructional Steel Research,2015(112) :54-60.
[4]Khaled M.EI-Sawy,Mohammad IKbal Martini Elastic stability of bi-axially loaded rectangular plates with a single circular hole[J].Thin-Walled Structures,2007(45) :122-133.
[5]N·E·Shanmugan,V·Thevendran,Y·H·Tan Design formulafor axially compressed perforated plates[J]. Thin - Walled Struc-tures,1999(34) :1-20.
[6]ANSYS Version 12.1[7] 徐芝纶。弹性力学[M].高等教育出版社,2006.

